Inter-Surface Maps via Constant-Curvature Metrics

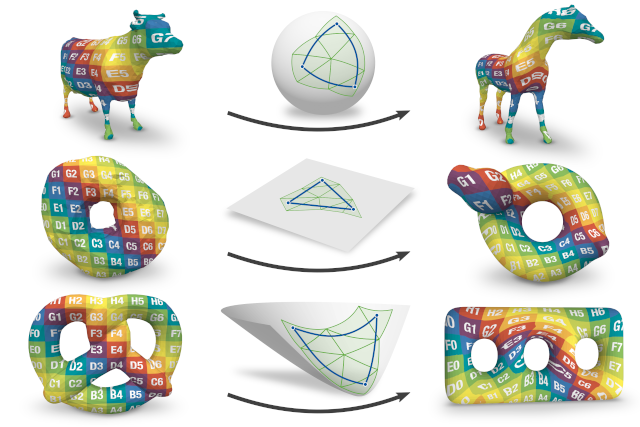
We propose a novel approach to represent maps between two discrete surfaces of the same genus and to minimize intrinsic mapping distortion. Our maps are well-defined at every surface point and are guaranteed to be continuous bijections (surface homeomorphisms). As a key feature of our approach, only the images of vertices need to be represented explicitly, since the images of all other points (on edges or in faces) are properly defined implicitly. This definition is via unique geodesics in metrics of constant Gaussian curvature. Our method is built upon the fact that such metrics exist on surfaces of arbitrary topology, without the need for any cuts or cones (as asserted by the uniformization theorem). Depending on the surfaces' genus, these metrics exhibit one of the three classical geometries: Euclidean, spherical or hyperbolic. Our formulation handles constructions in all three geometries in a unified way. In addition, by considering not only the vertex images but also the discrete metric as degrees of freedom, our formulation enables us to simultaneously optimize the images of these vertices and images of all other points.